Chi-quadrado
Origem: Wikipédia, a enciclopédia livre.
O coeficiente χ2 ou chi-quadrado é um valor da dispersão para duas variáveis de escala nominal, usado em alguns testes estatísticos. Ele nos diz em que medida é que os valores observados se desviam do valor esperado, caso as duas variáveis não estivessem correlacionadas.
Quanto maior o chi-quadrado (ou Qui-quadrado), mais significante é a relação entre a variável dependente e a variável independente.
Este valor está relacionado com uma distribuição, chamada Distribuição Chi-Quadrado.
A Distribuição Chi-quadrado com k graus de liberdade é a distribuição gama com parâmetros (k/2, 1/2).
Quanto maior o número de casos (n) ou o número de linhas ou colunas da tabela de contingência, maior será o Chi-quadrado. Por isso não faz sentido comparar o Chi-quadrado de duas relações entre variáveis. Para o efeito existem outros coeficientes, entre os quais ocoeficiente de contingência.
A distribuição Chi-quadrado pode ser simulada a partir da distribuição normal. Por definição, se  forem k distribuições normais padronizadas (ou seja, média 0 e desvio padrão 1) independentes, então a soma de seus quadrados é uma distribuição Chi-quadrado com k graus de liberdade:
forem k distribuições normais padronizadas (ou seja, média 0 e desvio padrão 1) independentes, então a soma de seus quadrados é uma distribuição Chi-quadrado com k graus de liberdade:
 forem k distribuições normais padronizadas (ou seja, média 0 e desvio padrão 1) independentes, então a soma de seus quadrados é uma distribuição Chi-quadrado com k graus de liberdade:
forem k distribuições normais padronizadas (ou seja, média 0 e desvio padrão 1) independentes, então a soma de seus quadrados é uma distribuição Chi-quadrado com k graus de liberdade:
Um corolário imediato da definição é que a soma de duas Chi-quadrado independentes também é uma Chi-quadrado:
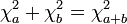
A fórmula do chi-quadrado é:

No link abaixo um resumo do pessoal da UFPA.


Nenhum comentário:
Postar um comentário